掘金同步 Tsp的理论与实践系列(6)更简洁的多起点的任务分配
tsp领域的问题, 并不都是tsp问题, 但是, tsp相关的算法一般都能解决, 只要你能为某一个充满个性的问题儿子找到他亲生的解决方案爸爸.
上一篇, 我们我们有一个克鲁斯卡尔的多起点的解决方案, 但是, 我们对他还有诸多不满, 因此在本期我们继续寻找更美的方案.
从数据结构的角度思考
- 每个订单都是一个队列(后续用q代替), 一个从起点到终点的队列, 某些订单甚至是一个3个点的队列.
- 因此, 我们每个订单都用一个q来表示. q里面的点每次只暴露一个出来, 也就是说起点没有被访问过的情况下, 终点是不可见的.
- 那么我们是否能定义q和q之间的距离呢? 答案是可以的.
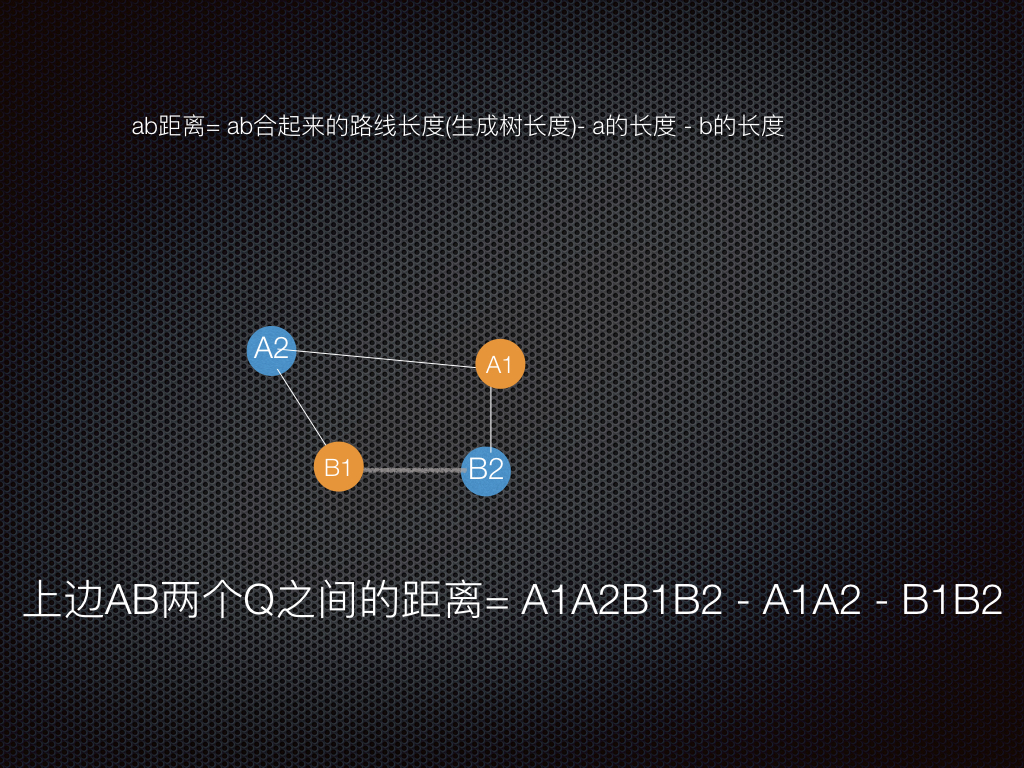
- 这里A1A2B1B2代表从A1到A2再到B1再到B2,
- 这里A1被指定为起点, 如果不指定起点, 那么要找最短的生成树, 以上图举例, 最小生成树为: B1B2A1A2
有了数据结构, 算法就变得很简单
用普利姆就可以解决问题, 每个司机自身也是一个Q, 他至少有一个出发地址. 而且, 这个出发地址是强制的起始点, 不论去哪里, 都要从当前的出发地址出发的.
多个司机构成一个森林, 按照q之间的距离, 逐步插入最短距离的q, 直到所有q都被插满, 或者司机都被耗尽, 某个司机的工作量被耗尽之后, 就把他从可以插的树里面剔除掉.
这样最终我们再次用普利姆生成树解决了这个配送分配问题, 不过别高兴得太早, 明天还有更严峻的考验在等着我们, 这一次生成树未必有用了, 预知后事如何, 请听下回分解.
注意, 这里并不是传统的人找单算法, 他和人找单的区别在于, 避免了人的顺序对分配的影响, 保证了最终生成的是最小生成树